Why Multiplication Strategies Are the Missing Bridge Between Models and Fact Recall

Resource featured: Multiplication Strategies Practice Pages

If you’ve ever watched a student perfectly build an array… and then freeze the second the numbers are written as 7 × 8, you already know what’s going on.

They understand multiplication conceptually… but they don’t yet have a reliable way to get to the answer without starting from scratch every time.

That’s exactly where multiplication strategies come in.

They’re not “shortcuts.” They’re the bridge.

The real problem isn’t effort... It’s the gap between understanding and recall

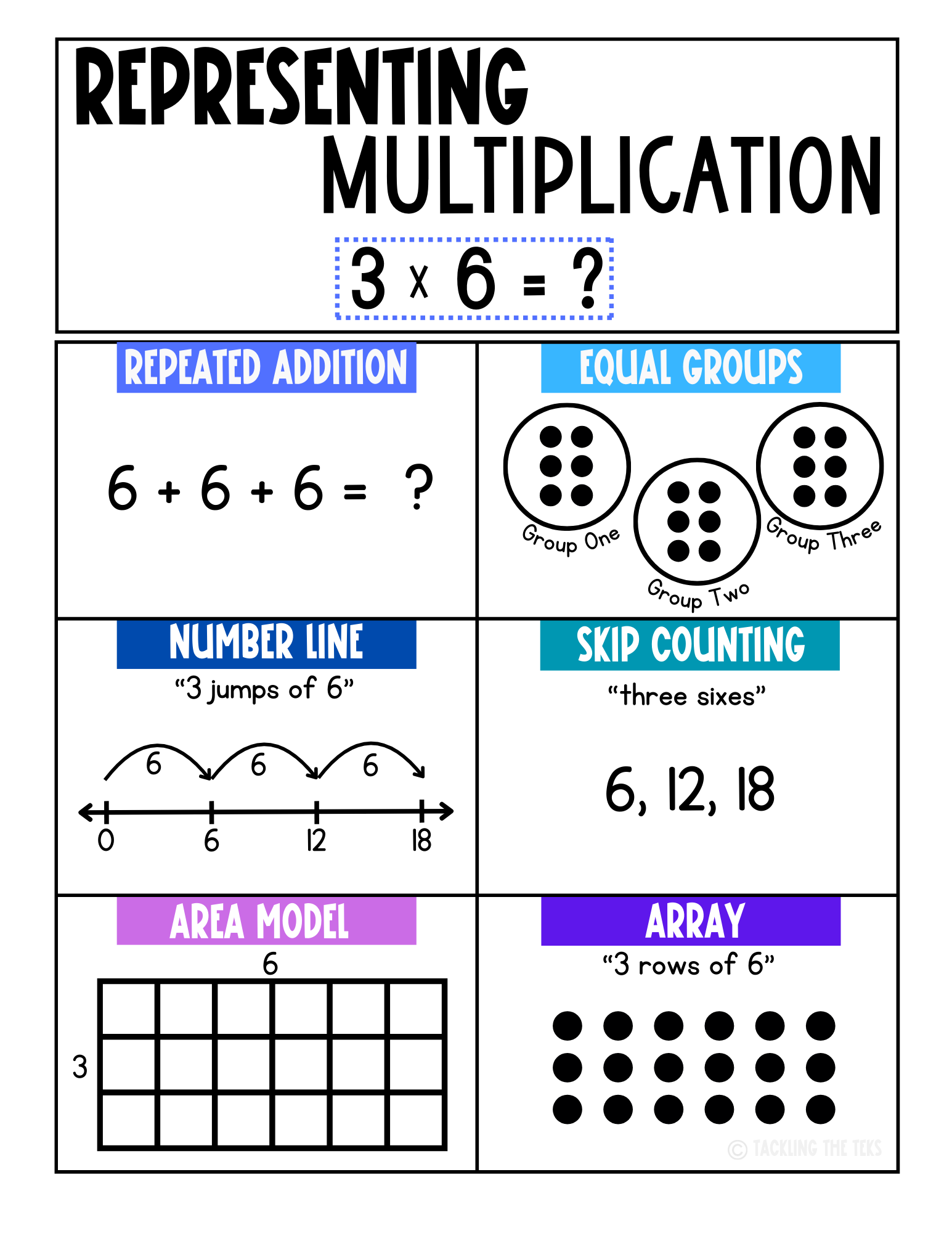
Most students start multiplication the way they should:

building equal groups
making arrays
skip counting
drawing pictures
using repeated addition

That’s the concrete and representational work that helps multiplication actually make sense.

But at some point, the math gets bigger:

multi-step problems
division
area models
fractions
long division
STAAR-style questions that assume facts are accessible

And if students are still drawing circles for every fact, the workload becomes overwhelming… fast.

So the goal isn’t “stop using models.”
The goal is: don’t make models the only plan.

CRA is the path and strategies are the bridge

CRA (Concrete → Representational → Abstract) doesn’t skip straight from drawings to instant recall. Students need something in the middle: a thinking plan they can rely on when memory fails.

Strategies give them that plan.

Instead of “I forgot,” students learn: “I can figure it out.”

And that matters because memory fails for everyone sometimes (even adults).

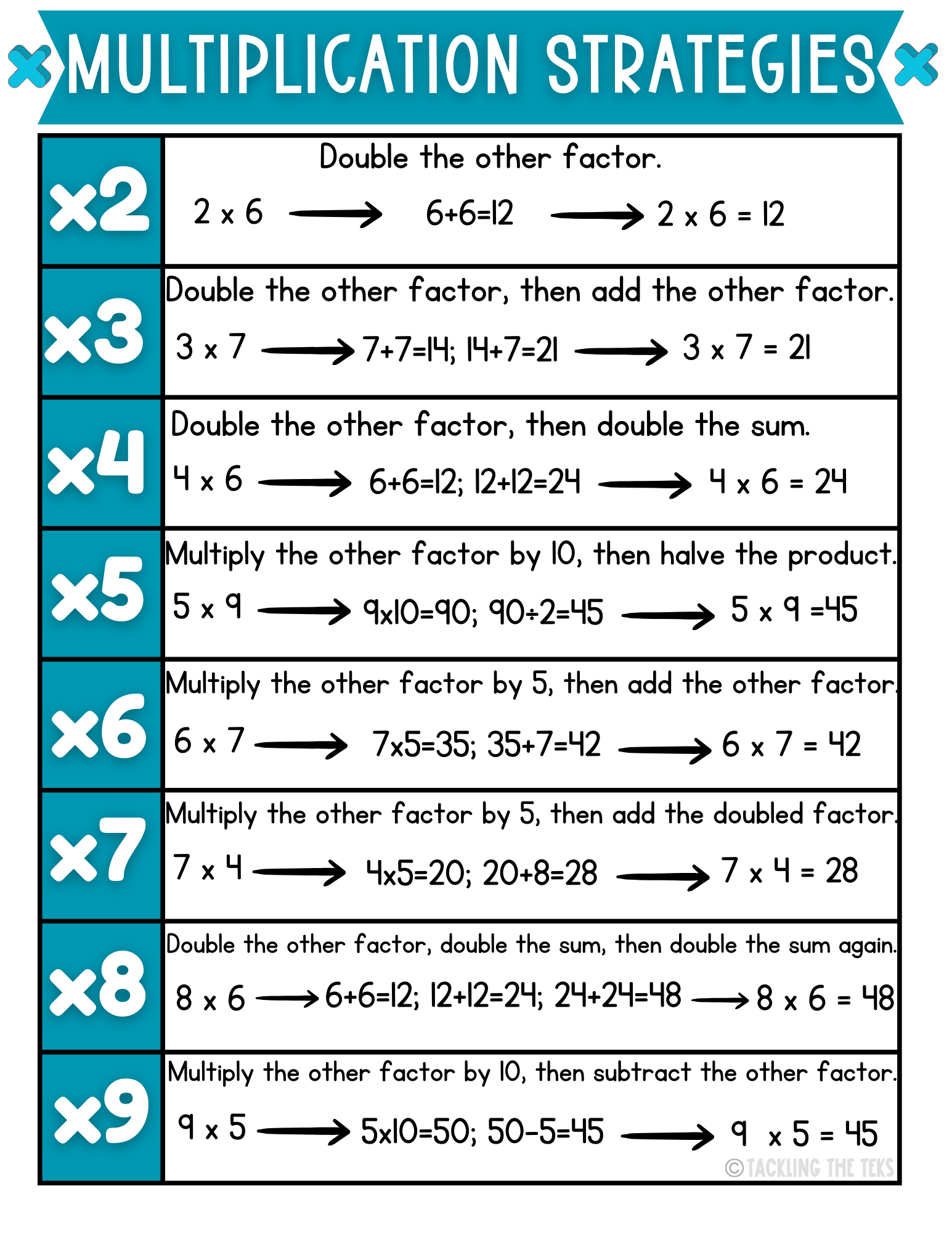
What strategy-based fluency sounds like

Strategy-based fluency means students can say things like:

“I don’t know 7×8 instantly, but I know 7×4, so I can double it.”
“I know 8×10 is 80, so 8×9 is one group of 8 less.”
“I know 6×6 is 36, so 6×7 is one more 6.”

This is the win: students aren’t stuck. They have a way forward. Over time, those relationships actually strengthen recall, because facts aren’t learned in isolation.

A simple way to teach strategies without taking over your block

You don’t need a whole “facts lesson” every day. Try 10–15 minutes:

Warm-up: quick strategy talk + 2 examples
Practice: students practice that strategy
Quick check: who’s ready to move on vs. who needs support

This works during stations, small-group intervention, morning work, or whenever you’ve got a short chunk of time.

Free resource: strategy explanations + practice

Want an easy way to start using strategies right away? Grab my free resource here:
👉Multiplication Strategies Practice Pages

Also check out Flexin' on the Facts: Multiplication Fluency Flow Workshop! (Math Bestie Members only!)